Caratteristiche e funzionamento della Rete di Feistel in sicurezza informatica

La Rete di Feistel

La Rete di Feistel è un algoritmo di cifratura a blocchi utilizzato in sicurezza informatica con una particolare struttura sviluppata dal crittologo dell’IBM Horst Feistel, moltissimi algoritmi di cifratura a blocchi la utilizzano, incluso il Data Encryption Standard (DES). La struttura inventata da Feistel ha il vantaggio che la cifratura e decifratura sono operazioni molto simili, spesso identiche, e che basta invertire il funzionamento del gestore della chiave per ottenere l’operazione inversa.

Operazioni fondamentali nella Rete di Feistel

La rete di Feistel utilizza le seguenti operazioni:

• Bit-shuffling (chiamata anche permutazione o P-box);
• Semplice funzione non lineare (chiamata anche S-box);
• Unione lineare (nel senso dell’algebra modulare) utilizzando lo XOR.

Queste operazioni, reiterate più volte (round), conferiscono alla rete di Feistel le proprietà di confusione e diffusione descritte da Claude Shannon.

Struttura di Feistel

Il blocco è lungo 2w bit, perché viene considerato come composto da 2 parti, ciascuna lunga w bit. Si hanno n fasi, e in ogni fase la parte di sinistra in output si chiama Ln, quella di destra Rn. La fase n prende in input le parti Ln-1 e Rn-1.

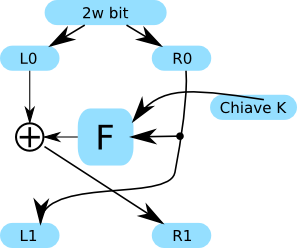
Ed ecco quello che succede:

• si prendono i 2w bit, e li si divide in 2 parti
• la parte R0 viene copiata in 2:
  • una copia entra nella F
  • l’altra copia diventa la L della fase successiva
• la parte L0 viene XORata con l’output della F
• il risultato dello XOR diviene la parte R della fase successiva

La F è la funzione di crittografia scelta. Inoltre, dopo l’ultima fase, di solito c’è un’ulteriore scambio per invertire le posizioni di Rn e Ln.

Ogni fase usa la Kn-esima chiave.

Nella struttura di Feistel compaiono sia le sostituzioni che le permutazioni. Si ha una sostituzione quando la parte L viene sostituita con lo XOR tra se stessa e l’output della F:

 L1 = L0 XOR F(R0, K0)

Abbiamo la permutazione quando, nell’ultima parte di ogni fase, inverto la posizione di Ln e Rn, dove Ln e Rn sono gli output di ciascuna fase.

Le reti di Feistel si caratterizzano per:

• dimensione del blocco
• dimensione della chiave
• numero di fasi
• algoritmo per generare le sottochiavi
• funzione F

Per decrittografare, si applica la stessa rete, partendo dal testo cifrato, ma usando le sottochiavi al contrario, ovvero nella prima fase uso l’ultima sottochiave usata nella crittografia, e così via.

Tutto questo Funziona? Sì. Ecco una struttura di Feistel ad 1 fase con il risultato dell’ultima fase scambiato di posto, come si è appena descritta.

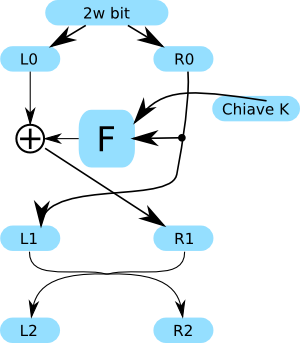
E adesso un po’ di conti. Per crittografare, si conosce L0, R0 e la chiave K

 L1 = R0
 R1 = L0 XOR F(R0, K)

 L2 = R1 = L0 XOR F(R0, K)
 R2 = L1 = R0

Ora, per decrittografare, si conosce solo R2, L2 e la chiave K, oltre che ovviamente l’algoritmo.

 R0 lo ottengo, perché ho R2, e so che R2 = L1 = R0
 So che L2 = R1 = L0 XOR F (R0, K) 
 => L2 = L0 XOR F (R0, K)
 => L0 = L2 XOR F (R0, K)
 L2 ce l'ho, R0 ce l'ho, K ce l'ho => so ricavare anche L0.

Se si applica tutto questo per tutte le fasi si riesce a risalire al messaggio originale.

Relazione con le reti sostituzione e permutazione (SP)

Una rete di Feistel può essere vista come una rete a sostituzione e permutazione (SP) in cui F è una SBox e lo scambio delle due metà è una P-Box. Le differenze principali rispetto alle reti SP sono che la chiave non è combinata direttamente in XOR col testo da cifrare, ma è un input della funzione F.